この内容は，Numerical Determination of the Field of Values of a General Complex Matrixを読んで実装したものです．
恐らくこの論文のアルゴリズム内の$\theta_j$は，$\theta_j = (j-1) / (2 \pi / k)$ではなく，$\theta_j = (j-1) * (2 \pi / k)$だと思います．
下記の内容に間違っている記述がある場合は，申し訳ありません．是非とも教えて頂けると嬉しいです．

線形方程式$Ax=b$のconvergence boundsを考えます．
一般には$A$の固有値で抑えたり，固有値分布で評価します．
またfield-of-valuesを用いて抑える手法もあります．
field-of-valuesは他にnumerical range，Wertovorrat，Hausdorff domain，range of valuesとも呼ばれるようです．
(Wikiではnumerical rangeですね)

field-of-valuesの定義は次式です． これは長さ$1$の単位ベクトルのRayleigh quotientのrangeと見れます． $$ F(A) = {x^* A x, x^*x = 1, x \in \mathbb{C}^n } $$

field-of-valuesは次の性質を持ちます．

  1. $F(A)$ is convex, closed and bounded.
  2. $\sigma(A) \subseteq F(A)$. ($\sigma(A)$ is set of eigenvalues.)
  3. $F(U^* A U) = F(A)$ for any unitary matrix.
  4. $F(A + zI) = F(A) + z$ and $F(zA) = zF(A)$ for any complex number $z$.
  5. If $A$ is hermite, then $F(A)$ is a segment of the real line $[\lambda_{min}, \lambda_{max}]$.
  6. If $A$ is normal, then $F(A)$ is $\text{Convex}(\sigma(A))$.

また，$A$のHermitian part($H(A)$)の最大固有値は，$F(A)$の境界に乗ります．
そのため，この最大固有値に対応する固有ベクトル$x$を用いて，$x^* A x$を計算すれば，$F(A)$の境界点が求まります．

この動作を$F(A)$を角度$\theta$で回転を繰り返し，境界点を求めていきます．
$F(A)$の$\theta$回転は$e^{i\theta}F(A)$ですが，これは$F(e^{i \theta}A)$なので(性質4)，$H(e^{i \theta}A)$の最大固有値，最大固有値に対応する固有ベクトルが分かれば良くなります．

求めた$F(A)$の境界点で凸多角形を作り，それを$F_{in}(A)$とします．
$F_{in}(A)$は必ず$F(A)$に内包されます．

また$F(A)$がconvexである条件を用いると(性質1)，回転角度$\theta_j$で求めた境界点$u$に対して，$F(A)$は直線$u+i\theta_{j}$を跨がないはずなので，$F(A)$を内包する凸多角形$F_{out}(A)$が作れます．

必ず$F(A)$は，$F_{in}(A)$と$F_{out}(A)$に挟まれているので，$F(A)$が存在する範囲を求めることができて
また，回転角度$\theta_j$を無限に小さくすれば$F(A)=F_{in}(A)=F_{out}(A)$になります．

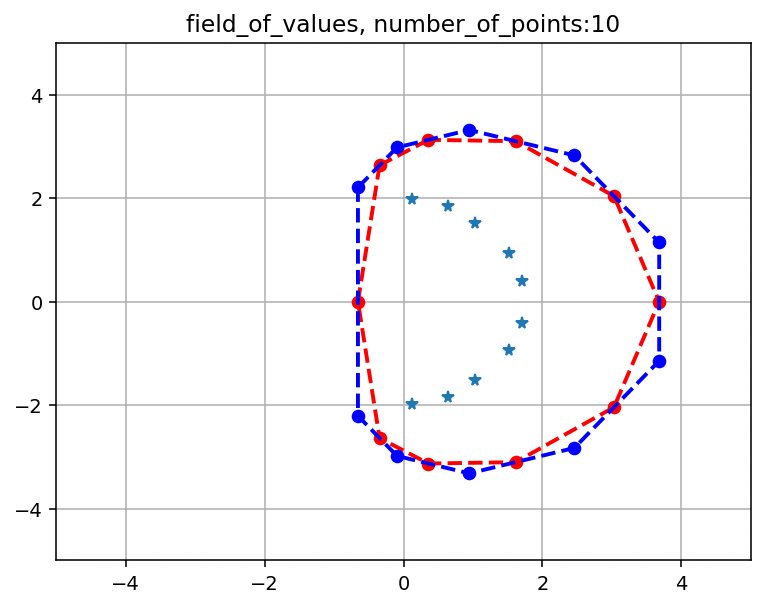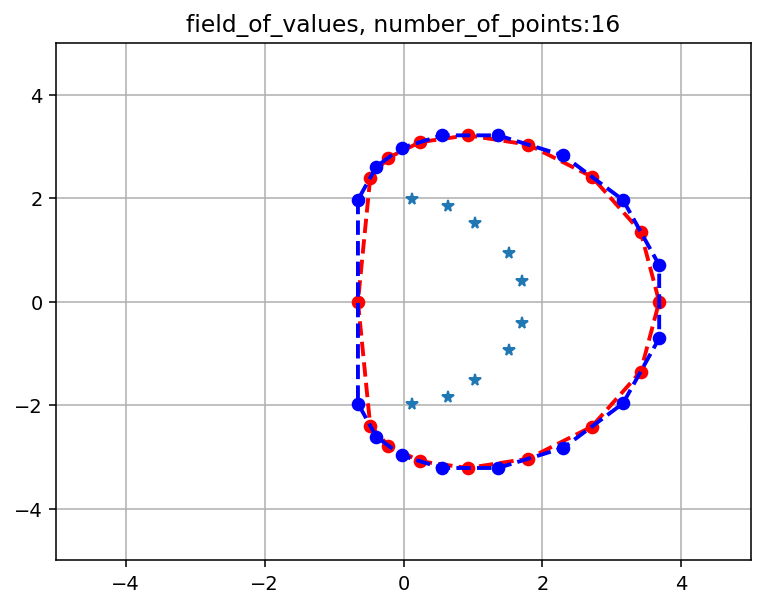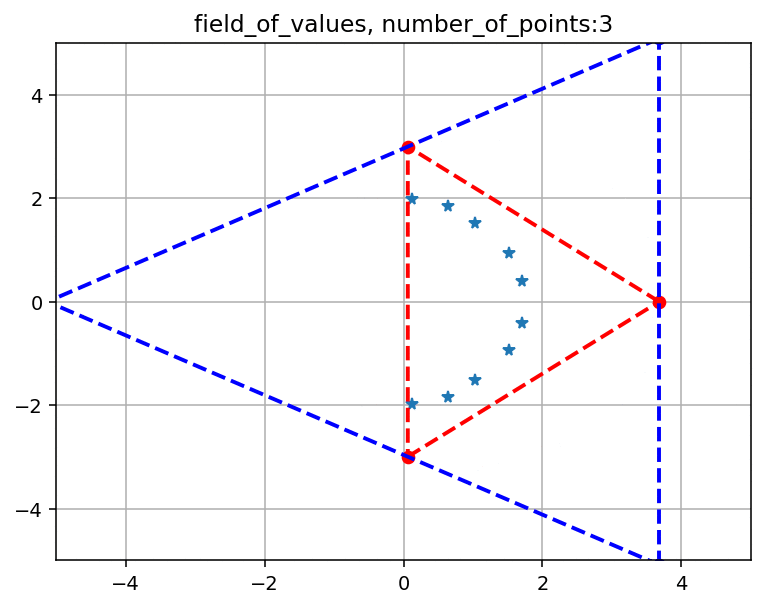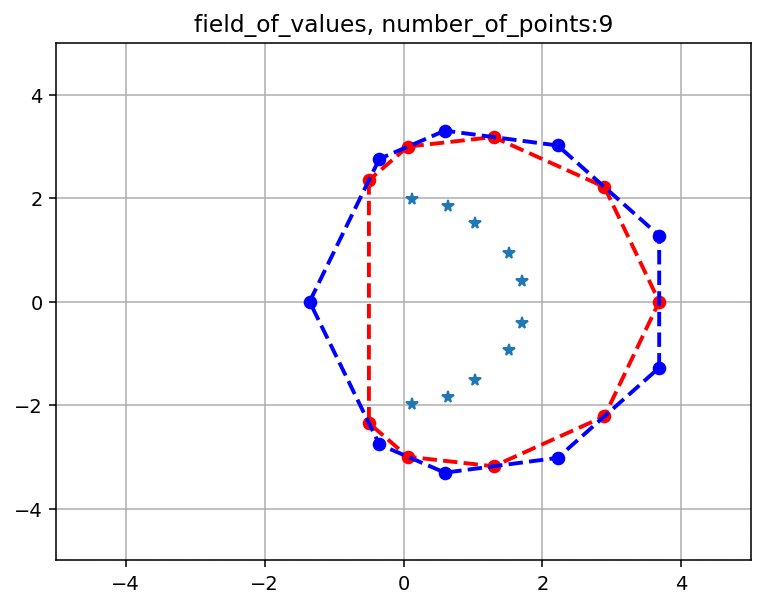
問題行列としてGRCAR(10, 5)で，$[0, 2\pi]$区間の分割数を$3 \sim 20$まで変えていった場合のプロットを乗せます．
青点はGRCARの固有値です．
赤点と赤点線で表される凸多角形は$F_{in}(A)$です．
青点と青点線で表される凸多角形は$F_{out}(A)$です．
つまり$F(A)$は赤と青の点線の間にあります．

$[0, 2\pi]$区間の分割数の終了条件は，次の面積比と，基準値$\epsilon$を決めます．
$$ \frac{\text{area}(F_{out}(A)) - \text{area}(F_{in}(A))}{\text{area}(F_{out}(A))} \leq \epsilon $$

また収束性解析では，$F(A)$の中で原点と最も距離が小さいものを$\nu(F(A))$として，$\nu(F(A))$と$\nu(F(A^{-1}))$を用います． $$ \frac{\|r_{n}\|}{\|r_{0}\|} \leq \left(1 - \nu(F(A)) \nu(F(A^{-1}))\right)^{\frac{n}{2}} $$

今回の例では$F(A)$に$(0, 0)$が入ってしまって，上手く見積もりとして用いられません．
その場合は多項式$\|p(A)\|$を用いて見積もるようです．

import numpy as np
import matplotlib.pyplot as plt
import scipy.linalg as LA

def H(B):
    B_star = np.conjugate(B.T)
    return 0.5 * (B + B_star)

def lambda_M(B):
    eig, vec = LA.eig(B)
    index = np.argmax(eig)
    return eig[index], vec[:, index]


def field_of_values(A, number_of_points, eps):
    n = len(A)

    # =========== 1. if A is hermitian
    is_hermite = True
    for i in range(n):
        for j in range(i+1, n):
            if abs(A[i, j] - A[j, i]) <= eps:
                continue
            is_hermite = False

    if is_hermite:
        eig, _ = LA.eig(A)
        poly = []
        poly.append(np.min(eig))
        poly.append(np.max(eig))
        return np.array(poly)

    # =========== 2. if A is normal
    is_normal = True
    AAT = np.dot(A, A.T)
    ATA = np.dot(A.T, A)
    
    for i in range(n):
        for j in range(n):
            if abs(AAT[i, j] - ATA[i, j]) <= eps:
                continue
            is_normal = False
    
    if is_normal:
        eig, _ = LA.eig(A)
        return eig

    # =========== 3.
    k = number_of_points  # Choose a k-mesh
    theta = []
    for j in range(0, k):
        theta.append((2*np.pi/k) * j)
    
    ps = []
    lambdas = []
    for j in range(len(theta)):
        # ===== Determine Fin: p_theta
        A_theta = np.exp(1j * theta[j]) * A
        HA = H(A_theta)
        lambda_theta, x_theta = lambda_M(HA)
        p_theta = np.dot(np.dot(np.conjugate(x_theta), A), x_theta)

        lambdas.append(lambda_theta)
        ps.append(p_theta)

    qs = []
    for j in range(len(theta)):
        # ===== Determine Fout: q_theta
        theta_one = theta[j]
        theta_two = theta[(j+1) % len(theta)]
        delta = theta_two - theta_one
        lambda_one = lambdas[j]
        lambda_two = lambdas[(j+1) % len(lambdas)]

        tmp = lambda_one + ((lambda_one * np.cos(delta) - lambda_two) / np.sin(delta)) * 1j
        q_theta = np.exp(-1j * theta[j]) * tmp
        qs.append(q_theta)
    
    return np.array(ps)

参考文献