この内容はNumerical Linear Algebra内の以下のLectureに相当します.
- Lecture 33, The Arnoldi Iteration
- Lecture 34, How Arnoldi Locates Eigenvalues
しかし,この本にはどのように多項式$p(z)$を求めるかが(明示的に)書いてありません.
また,自分のググり力では,多項式の求め方を見つけることができませんでした.
考えてみると,こうすれば多項式が求まるのでは,という方法がでました.
これが正しいのかは分かりませんが,結果をプロットしてみると,確かに性質を満たしていました.
もっとスマートな方法があるに違いないと思いますが,情報をまとめようと思いblogに書きました.
Arnoldi法
Arnoldi法とは,Krylov部分空間$\mathcal{K}(A, b)$に対して正規直交基底を求める方法です.
これは単純に$\mathcal{K}(A, b)$に対して,Modified Gram-Schmidtを適用し,直交基底を求める際の情報をHessenberg行列に格納するアルゴリズムです.
次の記号を導入します.$Q$は$n\times n$の正規直交基底です.$H$は$(n+1) \times n$のHessenberg行列で,上三角行列に下1行を追加した形です.
$$
Q_n = \left[ \begin{array}{c|c|c|c}
& & & \\
& & & \\
q_1 & q_2 & \cdots & q_n \\
& & & \\
& & & \\
\end{array} \right], \tilde{H}_n = \left[\begin{array}{cccc}
h_{11} & h_{12} & \cdots & h_{1n}\\
h_{21} & h_{22} & \cdots & h_{2n}\\
& \ddots & \ddots & \vdots\\
& & h_{n,n-1} & h_{n,n}\\
& & & h_{n+1,n}
\end{array}\right]
$$
Arnoldi法は以下の関係式を満たす,$Q_{n}, \tilde{H}_n$を求めます.
$$ A Q_n = Q_{n+1} \tilde{H}_n $$
具体的にどのように求めていくのか,それは次のコードのとおりです.
Q[:, 0] = b / la.norm(b)
for k in range(it):
u = A.dot(Q[:, k])
for j in range(k+1):
H[j,k] = np.dot(Q[:, j], u)
u = u - H[j,k] * Q[:, j]
H[k+1, k] = la.norm(u)
if H[k+1, k] <= EPS
break
Q[:, k+1] = u/H[k+1, k]
現在選ばれている全ての直交基底との射影成分を引くことで,新しい直交基底を選んでいます.
また基底$Q_j$方向のpowerをHessenberg行列の$H[j, k]$に格納しています.
$H[k+1, k]$に格納されるのは,現在の基底で表すことができなかったベクトルのノルムです.
つまり$H[k+1, k]$が$0$になれば,現在の基底で表す事が可能なので,新しい基底を作らずにループを抜けます.
射影での解釈
$Q^{*}_{n} Q_{n+1}$という行列を考えると,これは対角に$1$が並ぶ$n \times (n+1)$の行列です.
なぜなら$Q$は直交基底なので,$q_i$と$q_j$の内積は,$i == j$の時に$1$(正規),それ以外の時に$0$(直交)だからです.
そのため$Q^{*}_{n} Q_{n+1}\hat{H}_{n}$は,$n+1$行目を削除した$n \times n$の行列になります.
$$
Q^*_n Q_{n+1} \tilde{H}_n = H_n = \left[\begin{array}{cccc}
h_{11} & h_{12} & \cdots & h_{1n}\\
h_{21} & h_{22} & \cdots & h_{2n}\\
& \ddots & \ddots & \vdots\\
& & h_{n,n-1} & h_{n,n}\\
\end{array}\right]
$$
先に述べた式に戻り,左から$Q^{*}_{n}$をかける.
$$
A Q_n = Q_{n+1} \tilde{H}_n \\
Q^{*}_{n} A Q_n = Q^{*}_n Q_{n+1} \tilde{H}_n\\
Q^{*}_{n} A Q_n = H_n \hspace{3.0em}
$$
$Q_n$は$\mathcal{K}_n$の正規直交基底なので,$H_n$は$\mathcal{K}_n$上に$A$を射影した行列となります.
そのため$H_n$の固有値は,$A$の固有値と関係があります.
$H_n$の固有値は,$\textit{Arnoldi eigenvalue estimates}$,または$\textit{Ritz values}$と呼ばれ,$A$のスペクトル半径に近い固有値を近似します.
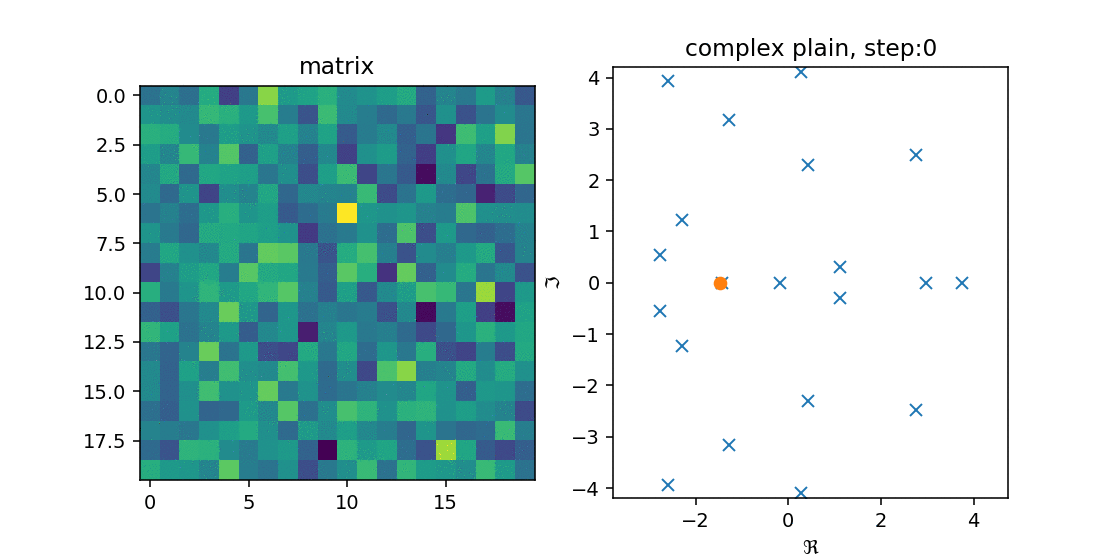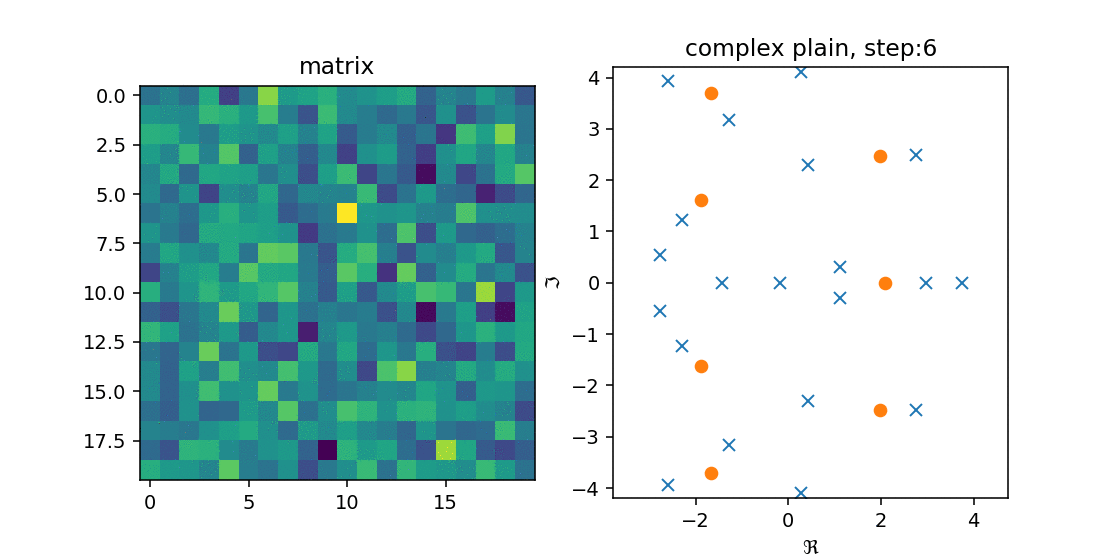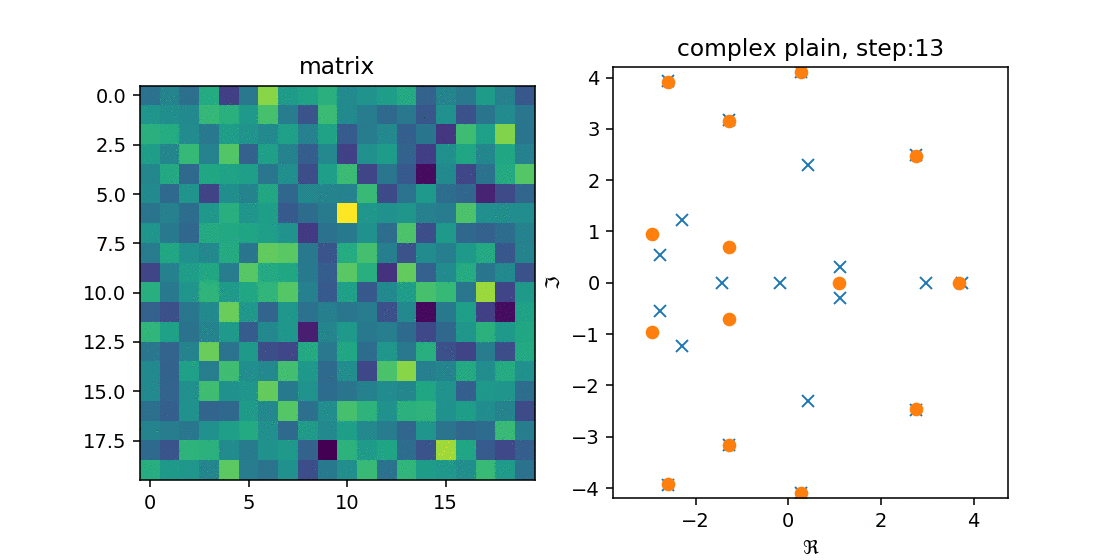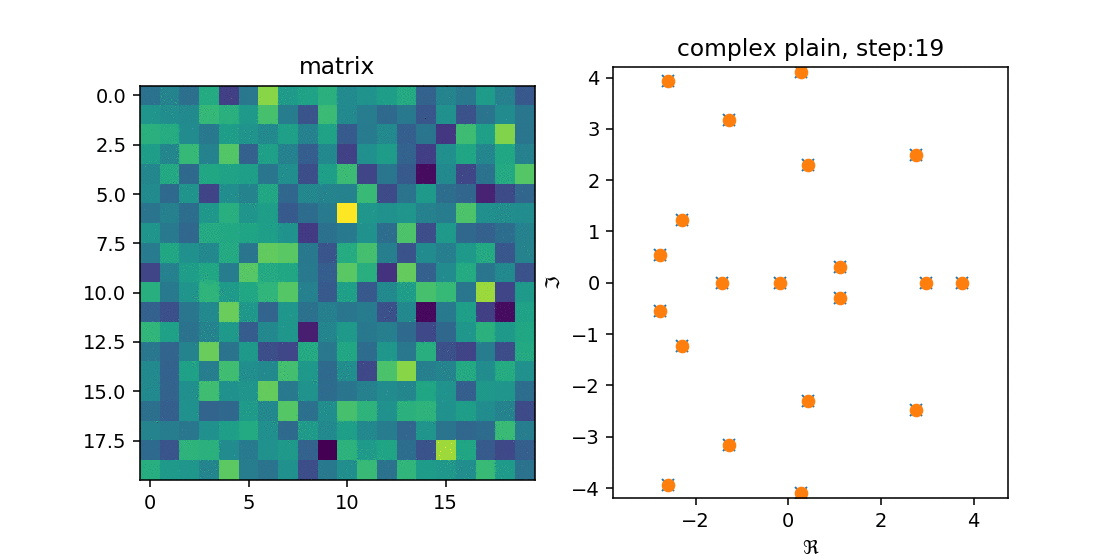
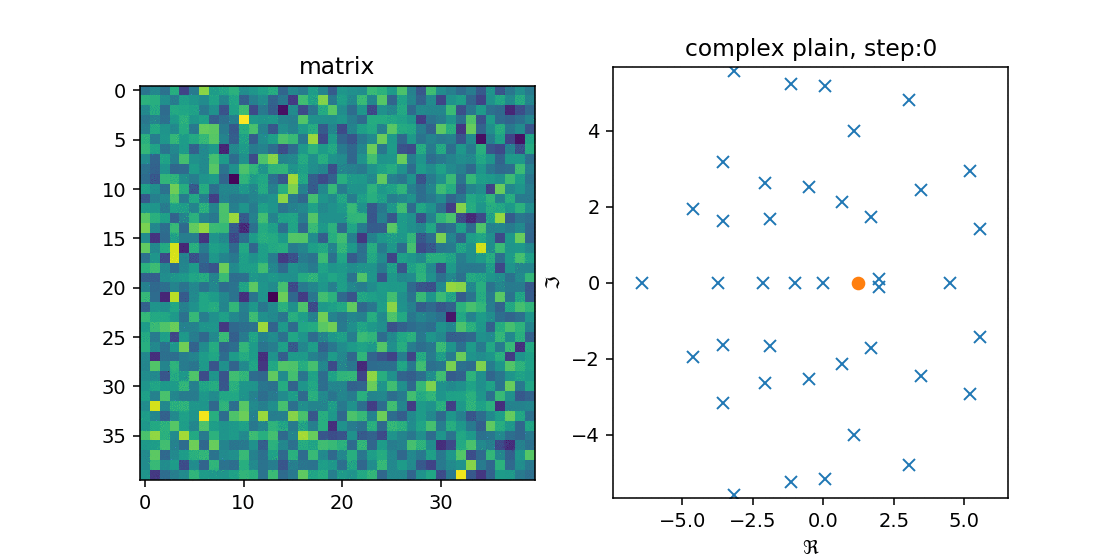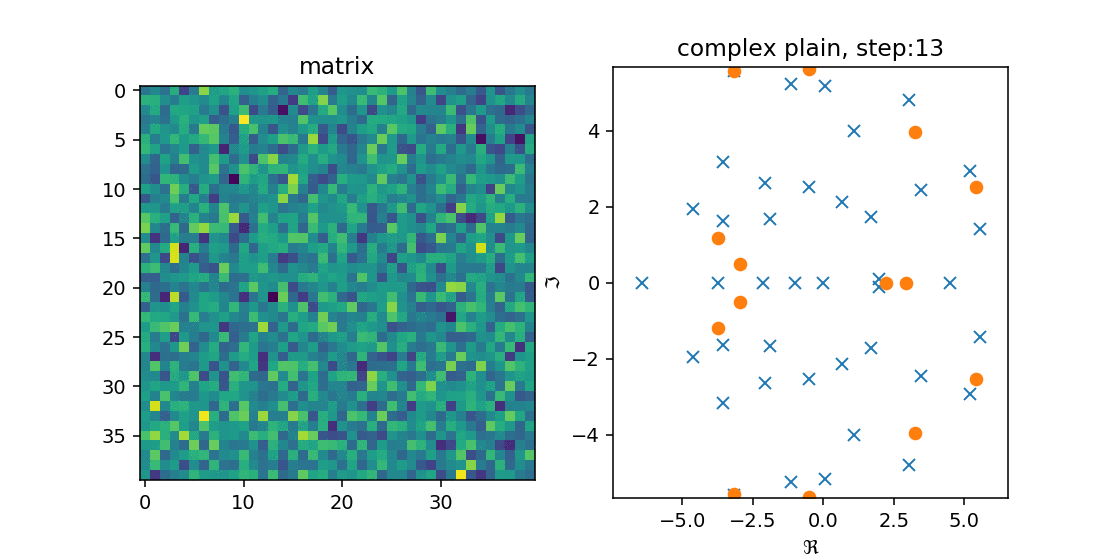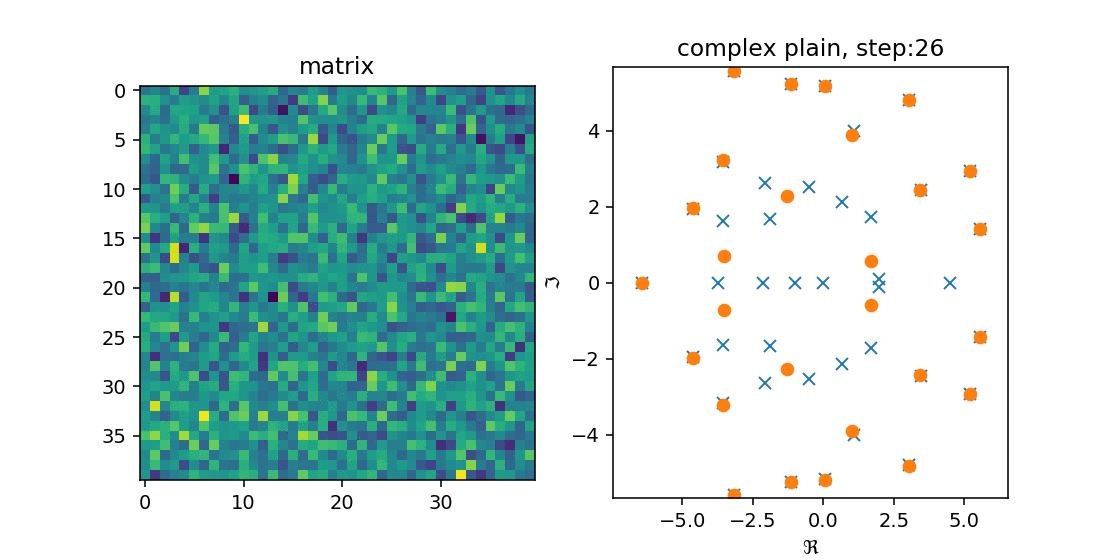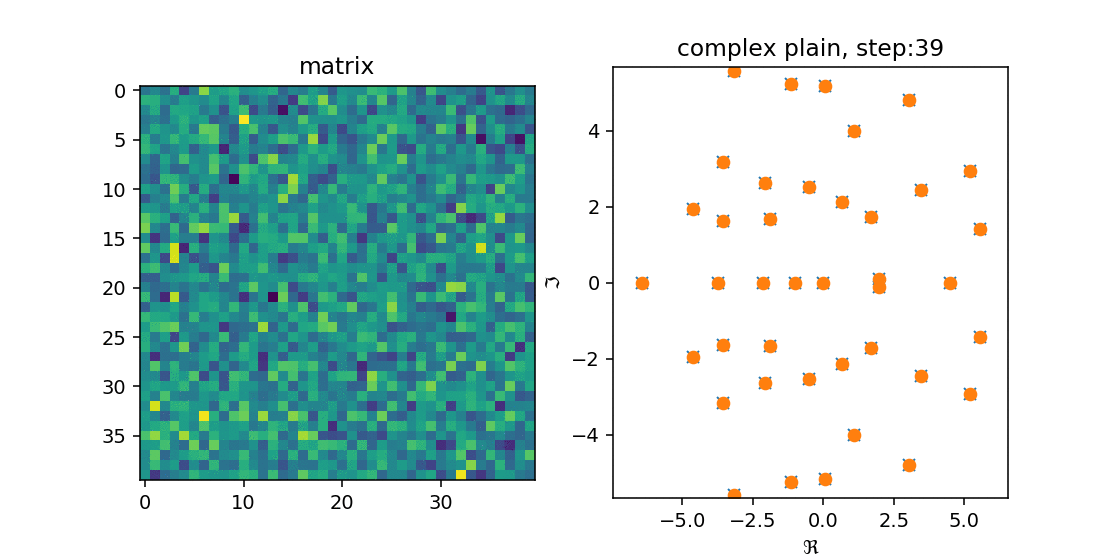
これを確かめるために,$n=25, 40$の時に$n \times n$の実数ランダム行列$A$を作成し,Arnoldi法を適用してみました.
右の図の青のxが$A$の固有値で,オレンジのoが$H_n$の固有値です.
左の図は$A$をimshowで出した結果です.
こうみると,徐々に固有値を近似していく($A$の固有値の上に収まる)様子が分かります.
Arnoldi法と多項式近似
Kyrolov部分空間$\mathcal{K}$上の任意のベクトルは次式で表せます.
$$ x = c_0 b + c_1 Ab + c_2 A^2 b + \cdots + c_{n-1} A^{n-1}b $$
ここで多項式$q(z)$を導入します.すると$x$は次のように書けます.
$$
q(z) = c_0 + c_1 z + \cdots + c_{n-1} z^{n-1}\\
x = q(A) b
$$
$q(z)$の中で$P^n$をmonicな$n$次多項式($n$次の項の係数が$1$)とした時,Arnoldi法は次の問題を解いていると見れます.
$$ \text{Find } p^n \in P^n, \text{such that } \|p^n (A) b\| = minimum $$
また$p^n \in P^n$の場合,$p^n(A)b = A^n b - Q_n y$となるので,次のような言い換えができます.
$$ \text{Find } y, \|A^n b - Q_n y\| = minimum $$
これを幾何学的に理解するには,p.260に載っている図が分かりやすいです.(引用 p.260 Figure 34.1 The least squares polynomial approximation problem underlying the Arnoldi iteration.)
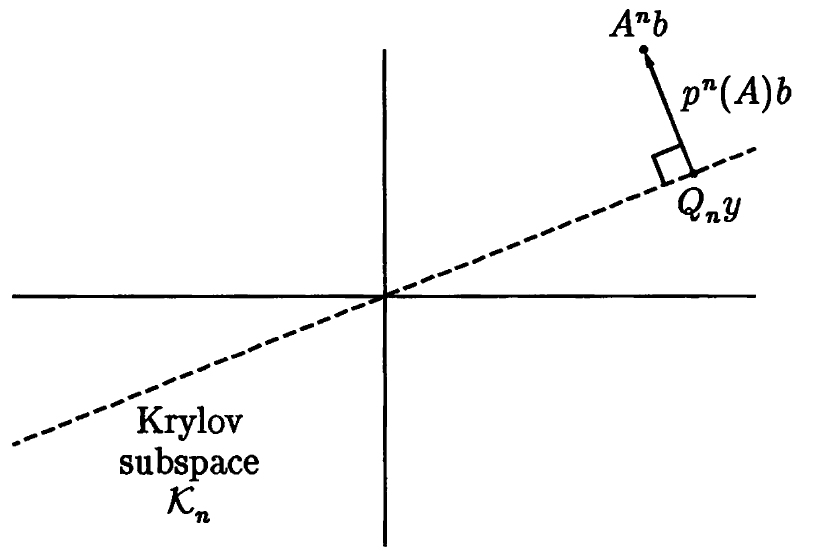
$A^n b$を見る時は,既に$n$本の直交基底$Q_n$で表現されるKyrolov部分空間$\mathcal{K}_n$があり,Krylov列/基底の$n+1$本目を見ている場合です.
つまり,この多項式$p(A)b$は,現在の基底$Q_n$で表せないベクトルを表しています.
そしてArnoldi法は,ベクトルの最小化を行ないます.
Arnoldi Lemniscates
Arnoldi法の収束過程は,複素平面に$\textit{lemniscates}$を描くことで幾何学的に見ることができます.
これは$\textit{Arnoldi lemniscates}$と呼ばれ,次の式で描くことができます.
$$
\{ z \in \mathbb{C} : |p(z)| = C\} \\
C = \frac{\|p^n (A) b \|}{\|b\|}
$$
さてここで本題となりますが,どのようにすれば$p(z)$を導出できるのでしょうか.
$p(z)$が分かるというのは,係数$c_0, c_1, …$が分かっているということです.
この係数を求めるために,以下の関係を列形式で書いて,$n=1, 2$の場合を見ていきます.
$$
A Q_n = Q_{n+1} \tilde{H}_n
$$
$$
A \left[ \begin{array}{c|c|c|c}
& & & \\
& & & \\
q_1 & q_2 & \cdots & q_n \\
& & & \\
& & & \\
\end{array} \right] = \left[ \begin{array}{c|c|c|c|c}
& & & &\\
& & & &\\
q_1 & q_2 & \cdots & q_n & q_{n+1} \\
& & & &\\
& & & &\\
\end{array} \right] \left[\begin{array}{cccc}
h_{11} & h_{12} & \cdots & h_{1n}\\
h_{21} & h_{22} & \cdots & h_{2n}\\
& \ddots & \ddots & \vdots\\
& & h_{n,n-1} & h_{n,n}\\
& & & h_{n+1,n}
\end{array}\right]
$$
$n=1$の時,$q_1 = \frac{b}{\|b\|}$を左辺にだけ代入します. $$ A q_1 = h_{11} q_1 + h_{21} q_2 \\
A \frac{b}{\|b\|} = h_{11} q_1 + h_{21} q_{2} \\
A b - \|b\|h_{11} q_{1} = \|b\|h_{21} q_{2} $$- これは$y_1 = \left[\|b\| h_{11} \right]$と見れば左辺は $$ A b - \|b\|h_{11} q_{1} = Ab - Q_1 y_1 $$
- となり,「$p^n \in P^n$の場合,$p^n(A)b = A^n b - Q_n y$」を用いれば,$Ab$の係数は$1$なので,右辺が$p^1(A)b$となります.
lemniscatesを書く際に求める$C$は,$\|p^n(A)b\|$を$\|b\|$で割るので,自然な感じがします. $$ \|b\|h_{21} q_{2} = p^1(A)b $$ - この右辺が$p^1(A)b$を表すことが分かったので,$c_0 b + c_1 Ab + \cdots + c_{n-1} A^{n-1}$の形にします.
$$
A b - \|b\|h_{11} \frac{b}{\|b\|} = \|b\|h_{21} q_{2} \\
p^1(A)b = - h_{11} b + A b $$ - $c_0 = -h_{11}$,$c_1 = 1$,$C = h_{21}$となり,これで$p(z) = C$を満たすlemniscatesが書けます.
$n=2$の時も同様,$q_{1} = \frac{b}{\|b\|}$,また上記の式から$q_2 = -\frac{h_{11}}{h_{21}\|b\|}b + \frac{1}{h_{21}\|b\|}Ab$を代入します. $$ A q_2 = h_{12} q_1 + h_{22} q_{2} + h_{32} q_{3} \\
A \left( -\frac{h_{11}}{h_{21}\|b\|}b + \frac{1}{h_{21}\|b\|}Ab \right) = h_{12} \frac{b}{\|b\|} + h_{22} \left( -\frac{h_{11}}{h_{21}\|b\|}b + \frac{1}{h_{21}\|b\|}Ab \right) + h_{32} q_3 \\
-\frac{h_{11}}{h_{21} \|b\|} Ab + \frac{1}{h_{21}\|b\|} A^2 b = \frac{h_{12}}{\|b\|}b - \frac{h_{11} h_{22}}{h_{21} \|b\|} b + \frac{h_{22}}{h_{21}\|b\|} Ab + h_{32} q_3 \\
-h_{11} Ab + A^2b = h_{12}h_{21}b - h_{11} h_{22} b + h_{22} Ab + \|b\|h_{21}h_{32} q_3\\
\|b\| h_{21}h_{32} q_3 = \left(-h_{12}h_{32} + h_{11}h_{22}\right)b + \left(-h_{11} + h_{22}\right) Ab + A^2 b $$- $c_0 = -h_{12} h_{32} + h_{11} h_{22}$,$c_{1} = -h_{11} + h_{22}$,$c_2 = 1$,$C = h_{21} h_{32}$
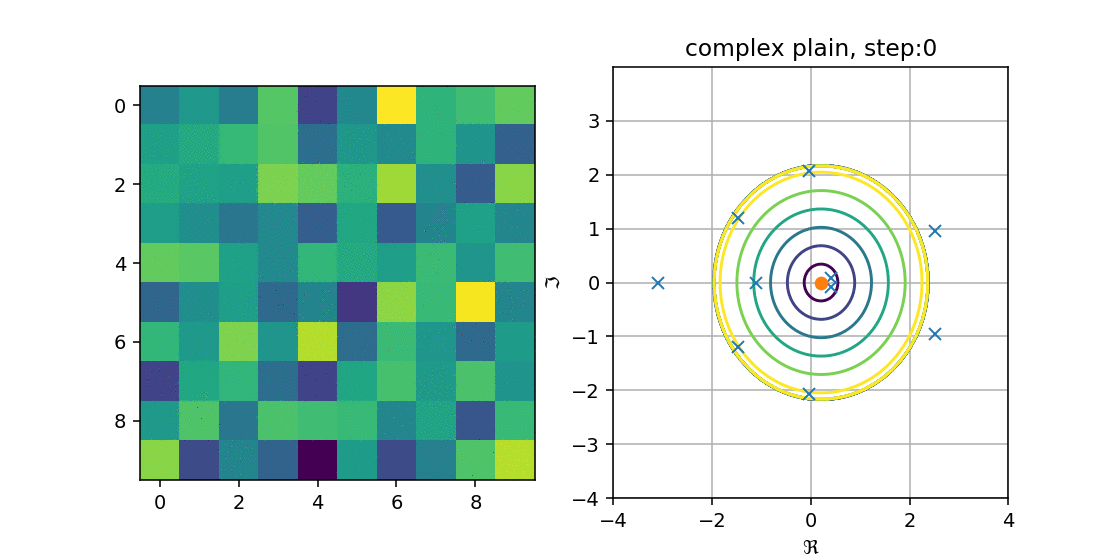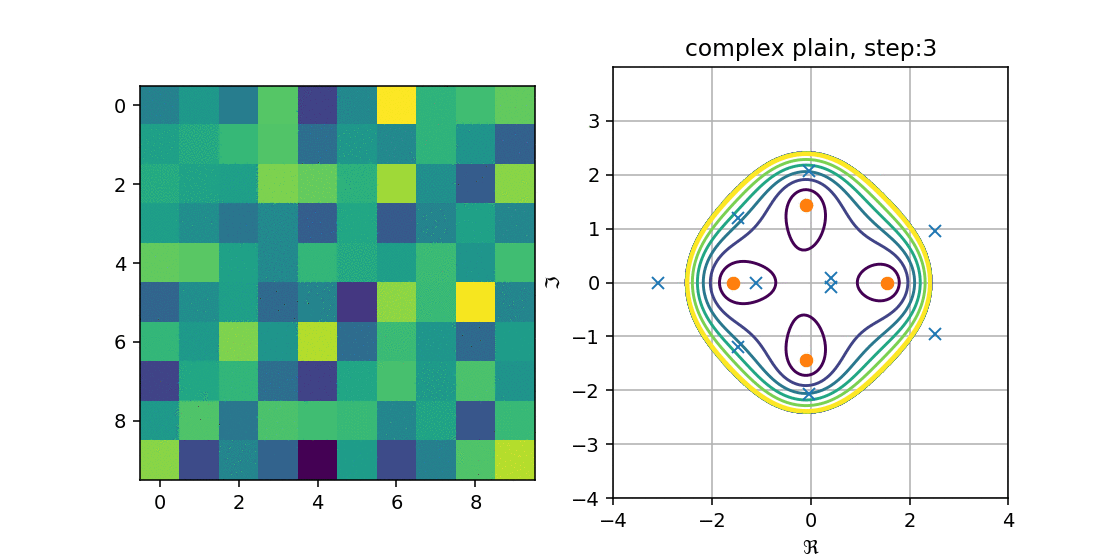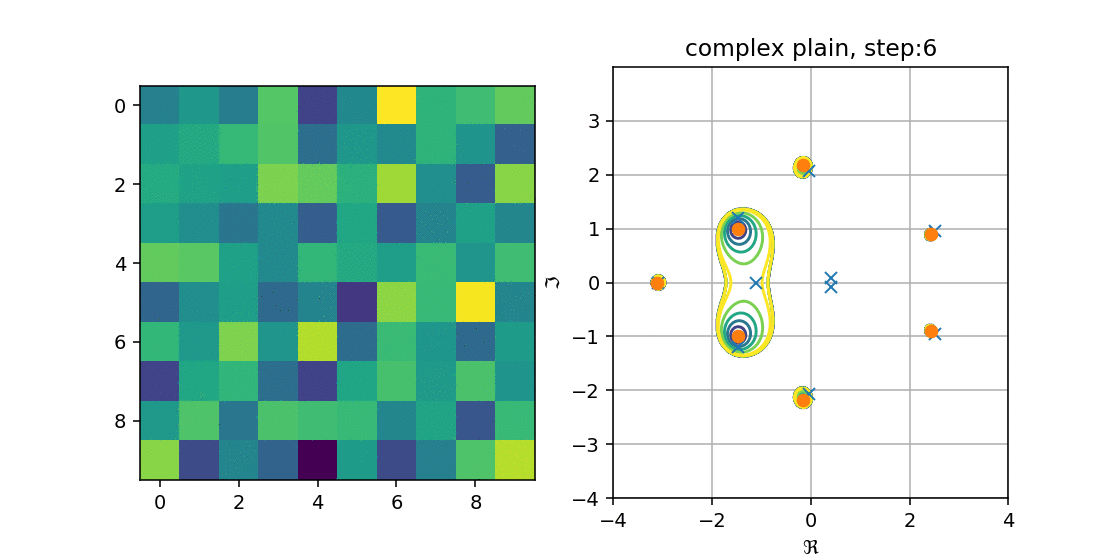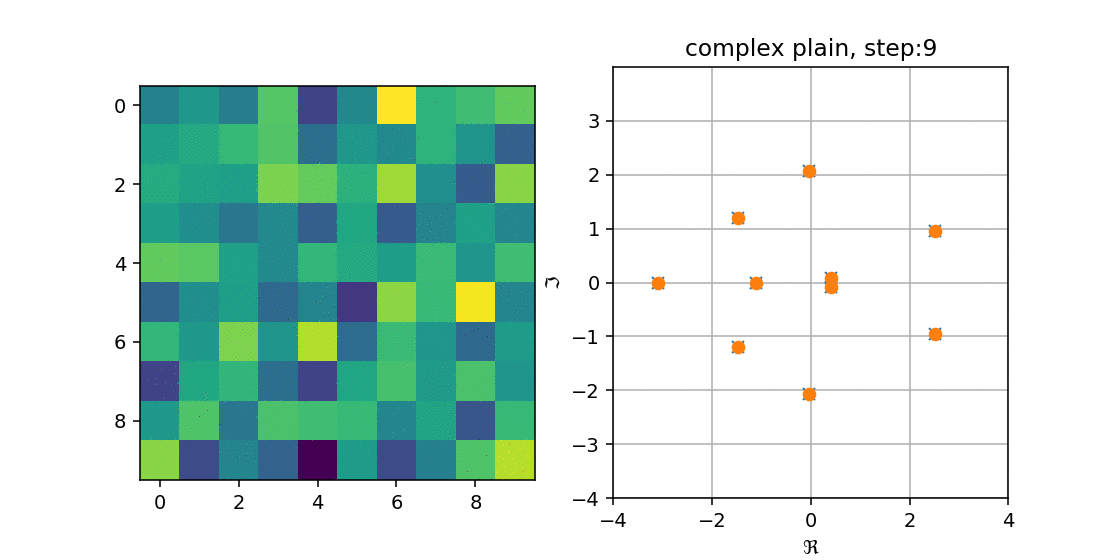
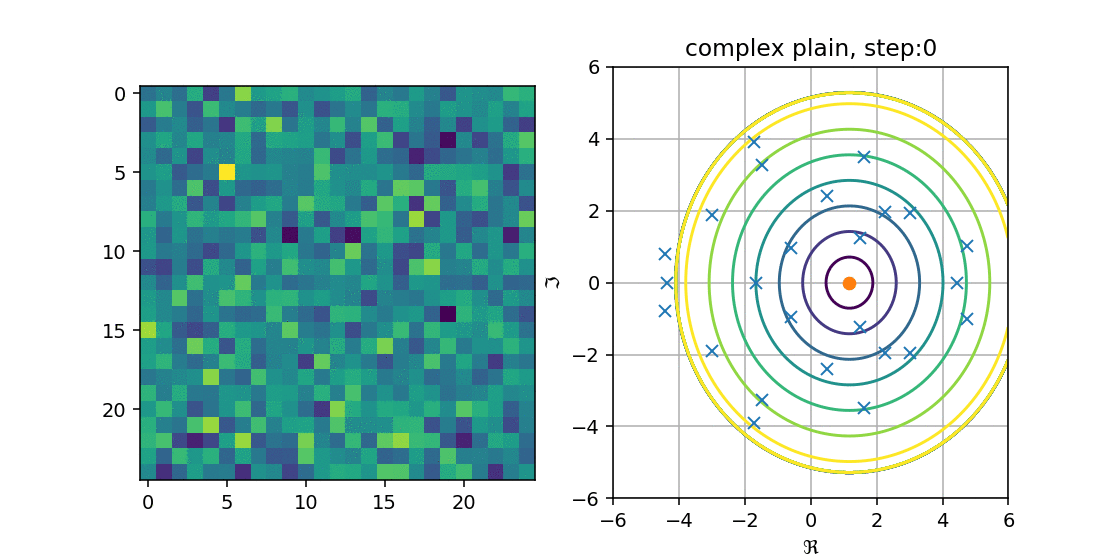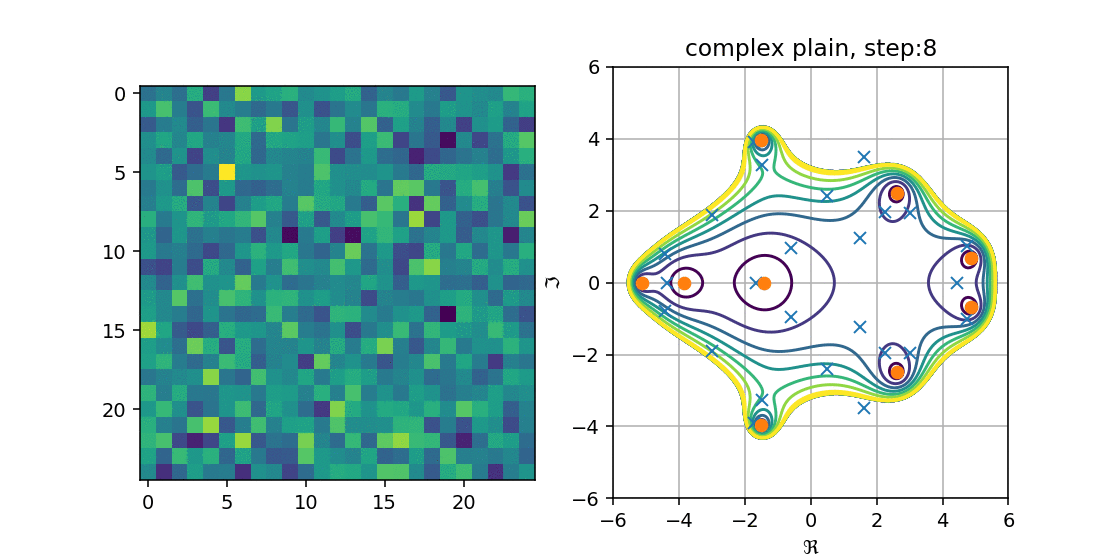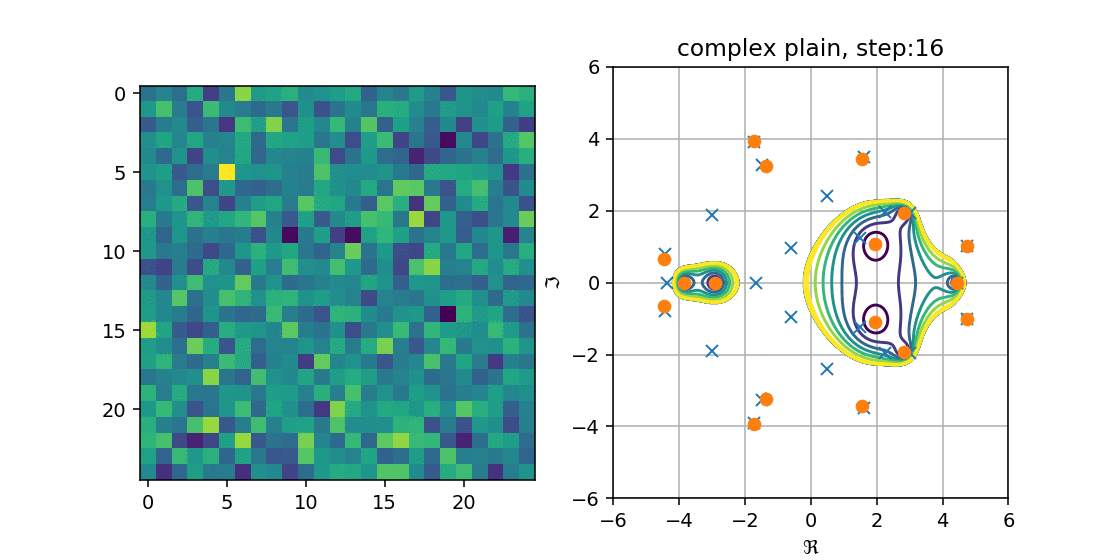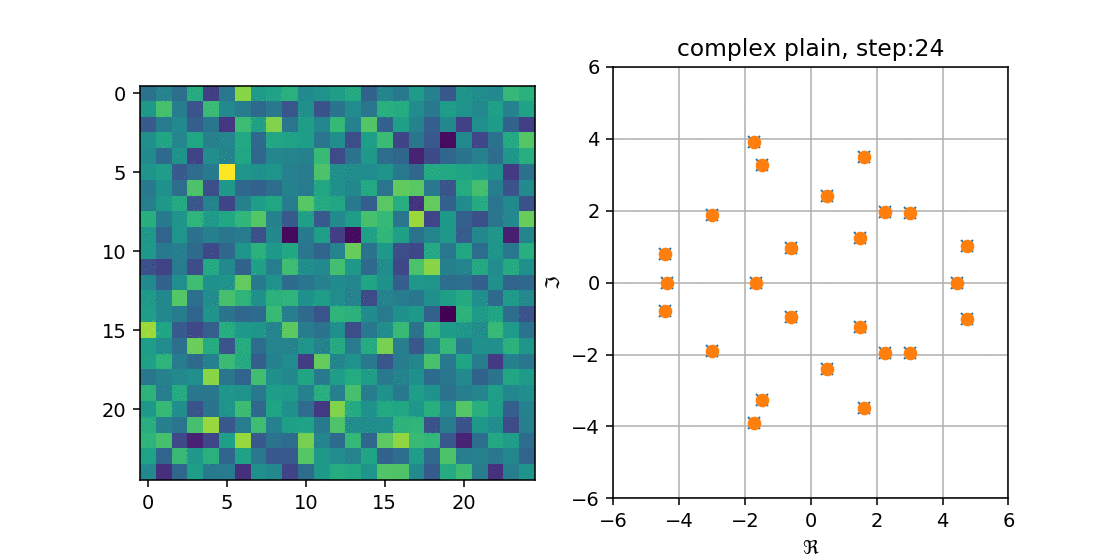
これを手順的に行って,プロットしたものが以下の図になります.
複素平面にメッシュを作り,$p(z)$の値が$C$以下の場合の等高線を出しました.
青が濃くなるほど値が小さく,一番濃い青に囲まれた箇所に近似固有値があることから
多項式の解がHessenbergの固有値になる,という性質を満たしているが分かります.
まとめ
間違っている記述がある場合は,申し訳ありません.
勉強をするので,是非とも教えていただけると嬉しいです.
多項式の導出には,もっとスマートな方法があるはずです.
もっと理解が深められるように進めていきます.