TopCoder Statistics - Problem Statement
This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

凸包が与えられる．隣り合わない点を選び，距離が$1$以下なら移動することができる．この条件の時に最大面積の増加分を答える

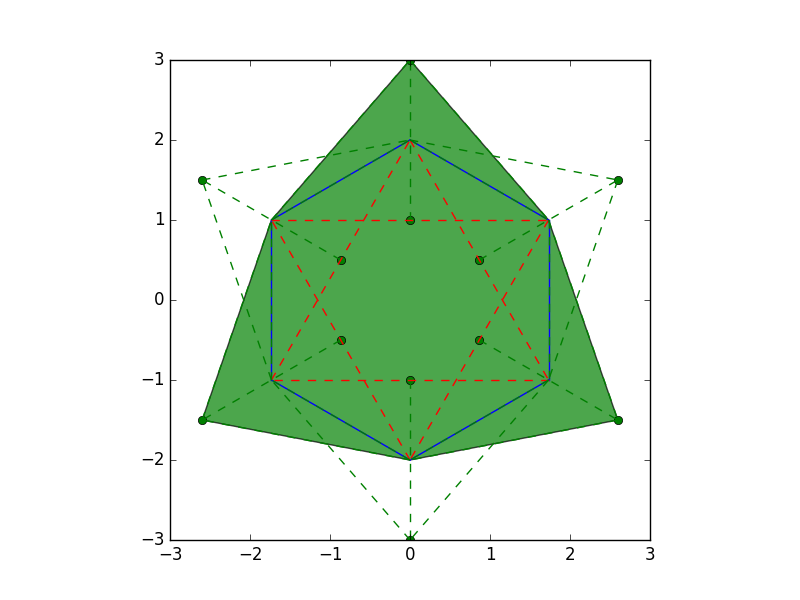
正六角形の場合を考えてみた．

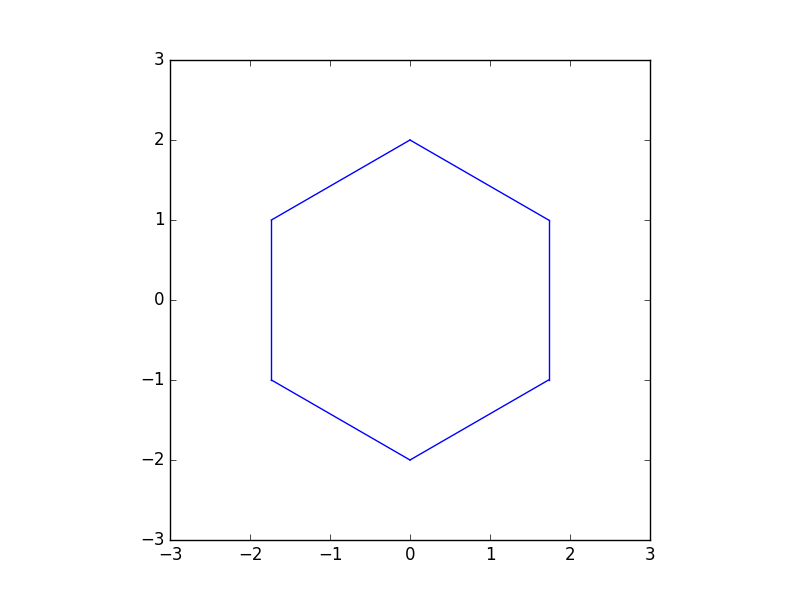
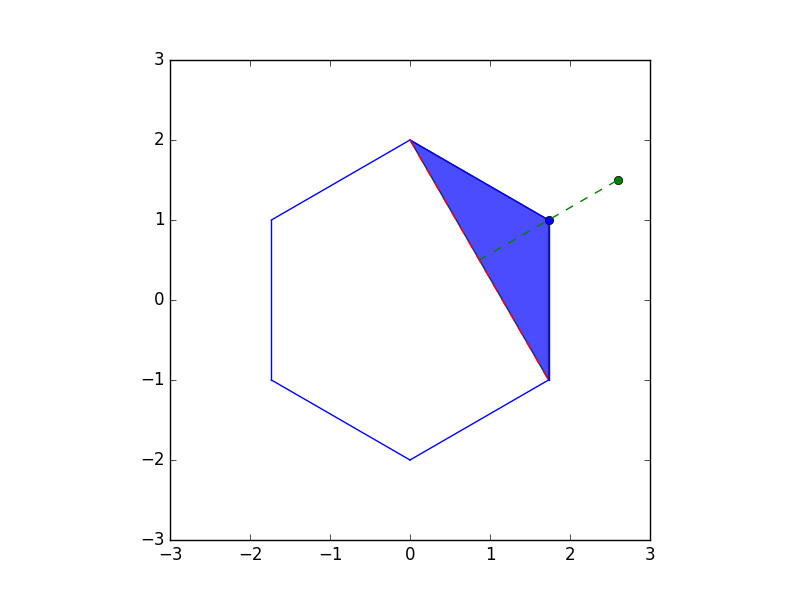
右上の点について考える．

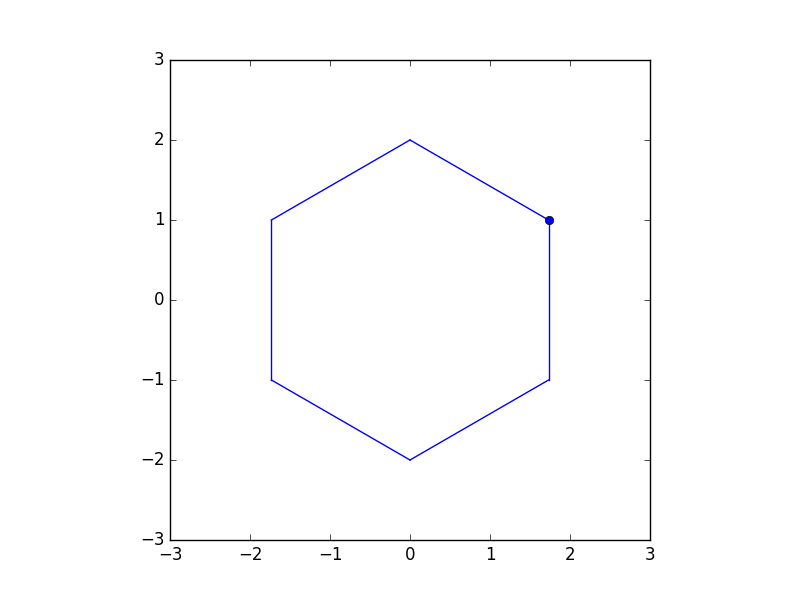
まずは移動しない場合の青の部分の面積を出してみる．

この面積を出すには赤の線を底辺$a$として，緑の線を高さ$h$とすると，$\frac{ah}{2}$である．

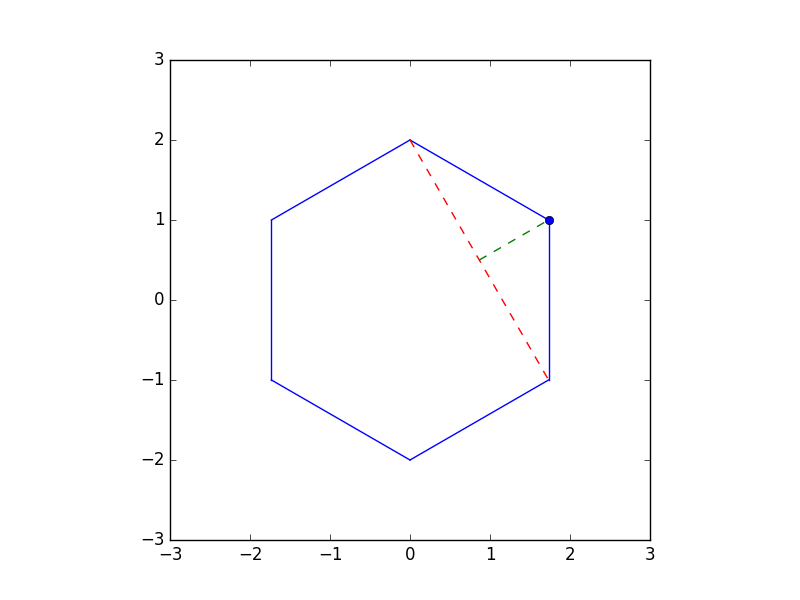
ここからこの点を移動することを考えるが，移動後の三角形もこの式で計算出来るため$h$を最大にすれば良い．最大の$h$とは，底辺に対して垂直に伸ばせば良いので，新しい三角形の高さは$h + 1$となる．つまり緑の点の場所に移動する．

次に面積の増加分を求める．増加した部分は緑の場所である．

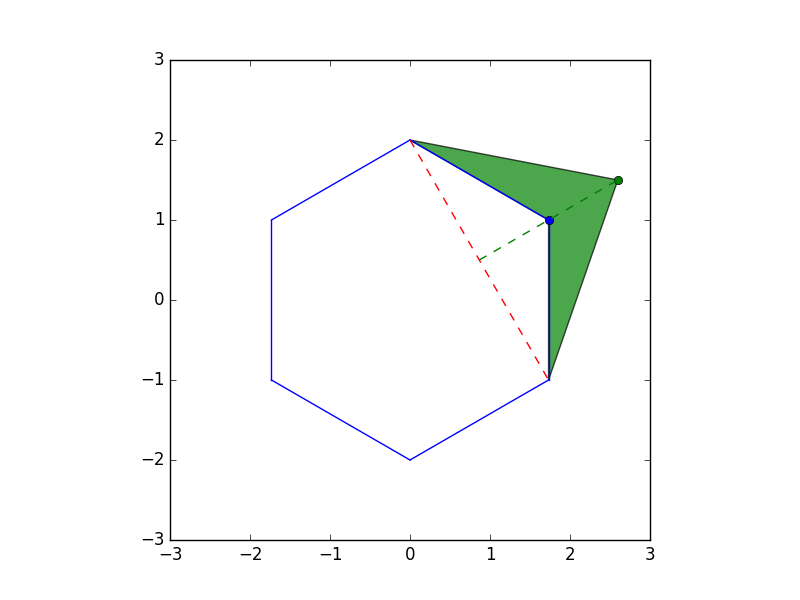
これは移動後の三角形(赤)から移動前の三角形(青)を引けば出てくる．

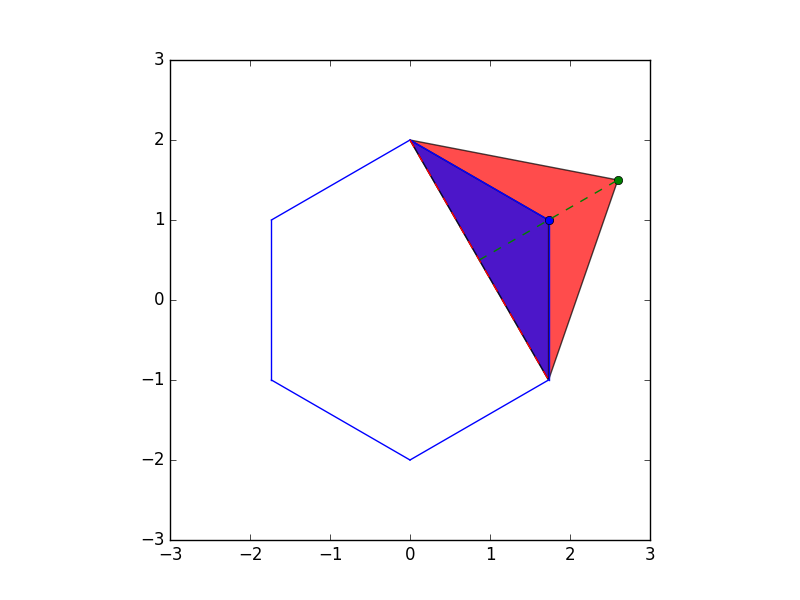
$\frac{a(h + 1)}{2} - \frac{ah}{2} = \frac{a}{2}$となり，高さが分かる必要がないことが分かる．後は移動する点が隣り合わないという条件を満たすようにdpで計算していく．

$$ dp[i][j] := 点_{i}まで見て，点_{i}を移動した場合はj=1, していない場合はj=0とした時の増加分の最大 $$

$0$と$n-1$番目が隣接しているため，$0$を使って$n-1$を見ないパターンと，$1$から始めて$n-1$まで見るパターンをやる．下の図は移動した場合の点が緑で，遷移が線となる．割り当てた状態をtextで書いてみた．

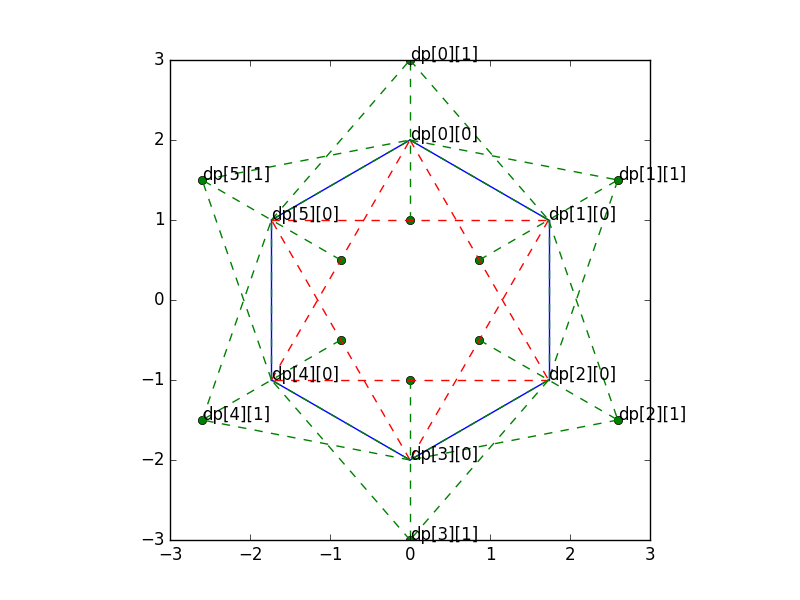
この場合は以下の$2$つが答えとなる．

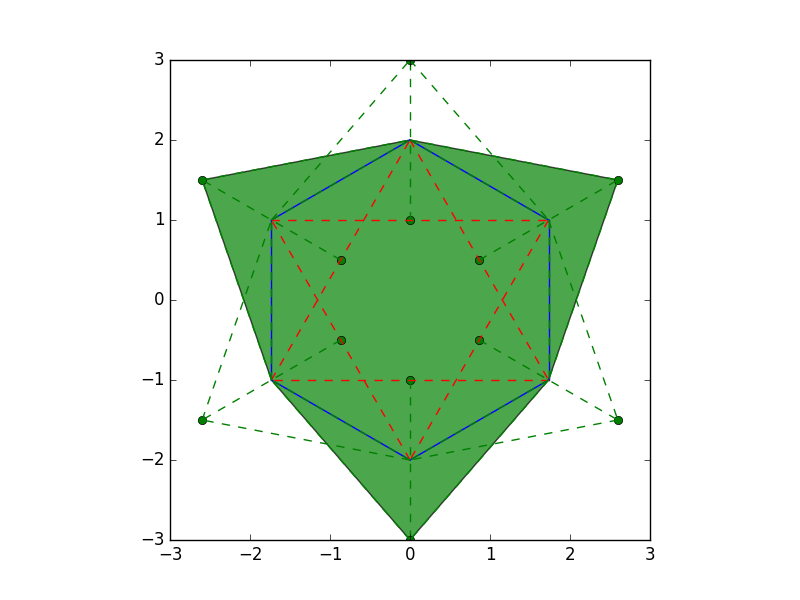
Code

#include <iostream>
#include <sstream>
#include <vector>
#include <string>
#include <cstring>
#include <algorithm>
#include <map>
#include <set>
#include <queue>
#include <cmath>

#define REP(i,k,n) for(int i=k;i<n;i++)
#define rep(i,n) for(int i=0;i<n;i++)
#define each(it,v) for(__typeof((v).begin()) it=(v).begin();it!=(v).end();it++)
#define INF 1<<30
#define mp make_pair

using namespace std;
typedef long long ll;
typedef pair<int, int> P;

double dp[55][2];

class PolyMove {
  public:
  double addedArea(vector <int> x, vector <int> y) {
      int n = x.size();
      memset(dp, 0, sizeof(dp));

      REP(i, 1, n) {
          int j = (i - 1 + n) % n;
          int k = (i + 1 + n) % n;

          dp[i][0] = max(dp[j][0], dp[j][1]);
          dp[i][1] = dp[j][0] + sqrt((x[j] - x[k]) * (x[j] - x[k]) + (y[j] - y[k]) * (y[j] - y[k]));
      }

      double ans = 0;
      rep(i, n) {
          rep(j, 2) {
              ans = max(ans, dp[i][j]);
          }
      }

      memset(dp, 0, sizeof(dp));
      rep(i, n - 1) {
          int j = (i - 1 + n) % n;
          int k = (i + 1 + n) % n;

          dp[i][0] = max(dp[j][0], dp[j][1]);
          dp[i][1] = dp[j][0] + sqrt((x[j] - x[k]) * (x[j] - x[k]) + (y[j] - y[k]) * (y[j] - y[k]));
      }

      rep(i, n) {
          rep(j, 2) {
              ans = max(ans, dp[i][j]);
          }
      }

      return ans / 2;
  }
};

ry0u_ydのblog

SRM304 D1E-D2H PolyMove

TopCoder Statistics - Problem Statement

Code