SRM691 D2M Sunnygraphs2

TopCoder Statistics - Problem Statement

Hero has just constructed a very specific graph. He started with n isolated vertices, labeled 0 through n-1. For each vertex i Hero then chose a vertex a[i] (other than i) and he added an edge that connected i and a[i]. This way he created a graph with n vertices and n edges.

　の 個の頂点で構成されるグラフがある．頂点 は頂点 と接続している．新しい頂点を加えることを考える．グラフの部分集合を選び，の の結ぶ辺をカットし， を接続する．これをした時に頂点が連結している部分集合の選び方はいくつあるか？

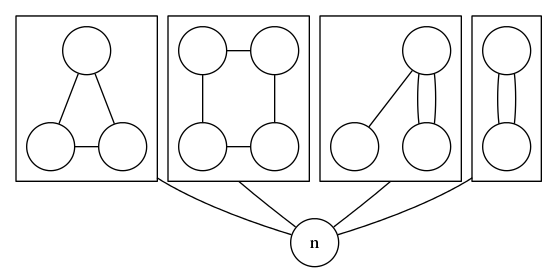
連結成分ごとで考える．全てを繋げたいので，それぞれの連結成分の中の組み合わせを掛けていけばよい．また，各頂点から必ず 本のみ結ぶ辺が出ているので，連結成分は必ず つの閉路を持つので，各連結成分の組み合わせの数は， となる(サイクルの方の組み合わせはサイクル全てを選ばないと全てが連結でなくなるので )．unionfindで連結成分を調べて，各連結成分ごとにdfsしてサイクル長を出した．

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <sstream>
#include <cstring>
#include <queue>
#include <set>
#include <map>

#define REP(i,k,n) for(int i=k;i<n;i++)
#define rep(i,n) for(int i=0;i<n;i++)

using namespace std;
typedef long long ll;

struct UnionFind {
  vector<int> par,rank;
  int N;

  UnionFind(int n) {
      N = n;
      par.resize(n);
      rank.resize(n);

      rep(i,n) {
          par[i] = i;
          rank[i] = 0;
      }
  }

  int find(int x) {
      if(par[x] == x) return x;
      else return par[x] = find(par[x]);
  }

  void unite(int x,int y) {
      x = find(x);
      y = find(y);

      if(x == y) return;

      if(rank[x] < rank[y]) {
          par[x] = y;
      }
      else {
          par[y] = x;
          if(rank[x] == rank[y]) rank[x]++;
      }
  }

  bool same(int x,int y) {
      return find(x) == find(y);
  }

  int size() {
      int cnt = 0;
      rep(i,N) if(find(i) == i) cnt++;
      return cnt;
  }
};

vector<int> g[105];
int d[105];

int dfs(int cur) {
  rep(i, g[cur].size()) {
      int t = g[cur][i];
      if(d[t] != -1) {
          return abs(d[t] - d[cur]) + 1;
      }
      d[t] = d[cur] + 1;
      return dfs(t);
  }
  return 0;
}

class Sunnygraphs2 {
  public:
  long long count(vector <int> a) {
      int n = a.size();
      rep(i, 105) g[i].clear();

      UnionFind uf(n);
      rep(i, n) {
          uf.unite(i, a[i]);
          g[i].push_back(a[i]);
      }

      int m = uf.size();

      map<int, vector<int> > ma;
      rep(i, n) {
          ma[uf.find(i)].push_back(i);
      }

      ll ans = 1;
      map<int, vector<int> >::iterator ite;

      for(ite = ma.begin(); ite != ma.end(); ite++) {
          int root = ite->first;
          vector<int> v = ite->second;

          memset(d, -1, sizeof(d));
          d[root] = 0;

          rep(i, 105) g[i].clear();
          rep(i, v.size()) {
              g[v[i]].push_back(a[v[i]]);
          }
          int len = dfs(root);

          ll cy = 1;
          rep(i, len) cy *= 2;
          cy--;

          ll res = 1;
          rep(i, v.size()-len) res *= 2;

          cy *= res;
          ans *= cy;
          continue;
      }

      if(m == 1) ans++;
      return ans;
  }
};
May 31st, 2016
srm, topcoder, unionfind, グラフ, 閉路