SRM683 D2H SubtreesCounting

TopCoder Statistics - Problem Statement

You are given an undirected tree T. (The input format is specified below.) The vertices of the tree are numbered 0 through n-1. A subtree of T is any subgraph of T that is connected. The size of a subtree is the number of vertices it contains.

Sample1

Sample1で構成される木は である．この木の全ての部分木の頂点数は

頂点数

頂点数

頂点数

よってである．

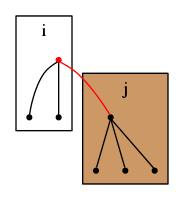
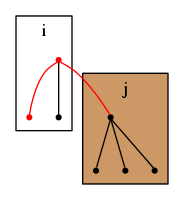
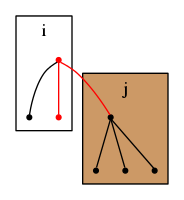
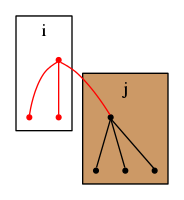
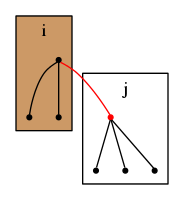
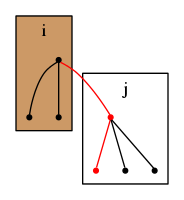
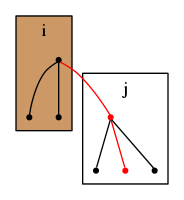
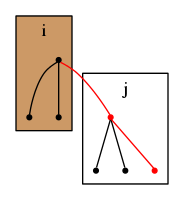
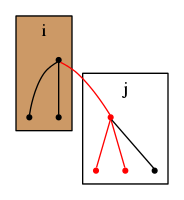
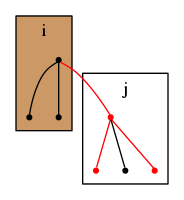
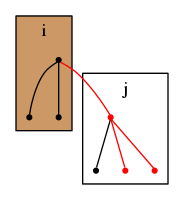
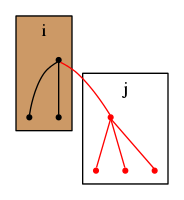
頂点を根とする木に頂点を根とする木を付け加える場合を考える．
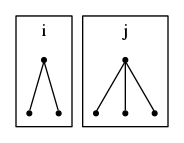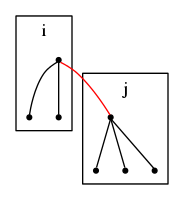を としたい．
この時，

とすると，頂点数だけ増加する．



同様に部分木の個数だけ増加する．適当に根を決め，潜って元の頂点に戻る時に足していく．自分の全ての子を潜り終わったらそれ以上変更があることはないので数える．

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

struct edge {
  int from,to;
  int cost;

  edge(int t,int c) : to(t),cost(c) {}
  edge(int f,int t,int c) : from(f),to(t),cost(c) {}

  bool operator<(const edge &e) const {
      return cost < e.cost;
  }
};

vector<edge> G[100005];
ll dp[100005], num[100005], cnt[100005];
bool used[100005];

void dfs(int cur) {
  used[cur] = true;
  dp[cur] = 1;
  num[cur] = 1;
  
  rep(i, G[cur].size()) {
      int to = G[cur][i].to;
  
      if(!used[to]) {
          dfs(to);

          dp[cur] += (dp[cur] * num[to]) + (dp[to] * num[cur]);
          num[cur] += num[cur] * num[to];
  
          dp[cur] %= MOD;
          num[cur] %= MOD;
      }
  }
  
  cnt[cur] = dp[cur];
}

class SubtreesCounting {
  public:
  int sumOfSizes(int n, int a0, int b, int c, int m) {

      rep(i, 100005) G[i].clear();

      vector<ll> v(n);
      v[0] = a0;

      REP(i, 1, n-1) {
          v[i] = (b * v[i-1]) % m + c;
          v[i] %= m;
      }

      REP(i, 1, n) {
          int j = v[i-1] % i;
          G[i].push_back(edge(j, 1));
          G[j].push_back(edge(i, 1));
      }

      memset(dp, 0, sizeof(dp));
      memset(num, 0, sizeof(num));
      memset(cnt, 0, sizeof(cnt));
      memset(used, 0, sizeof(used));

      dfs(0);

      ll ans = 0;
      rep(i, n) {
          ans += cnt[i];
          ans %= MOD;
      }

      return ans;
  }
};
Mar 4th, 2016
srm, topcoder, 木