Codeforces311-div2C Arthur and Table

http://codeforces.com/contest/557/problem/C

足の長さがバラバラなのでこれを安定状態にしたい．安定状態になるには足の最大の長さの本数が全体の本数の半分より多ければよい．その時の最小のコストを求める．

Sampleを考える．長さ1を1マスとし，文字がコストを表す．取り除いた足を赤色で表現する．

Sample1

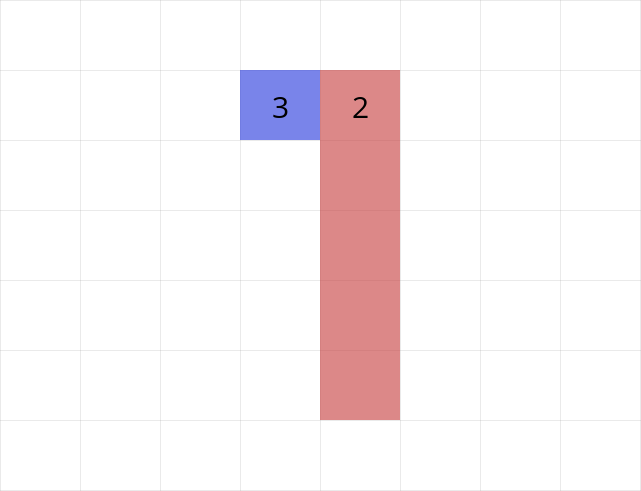
長さ5を取り除くほうがコストが安い

Sample2

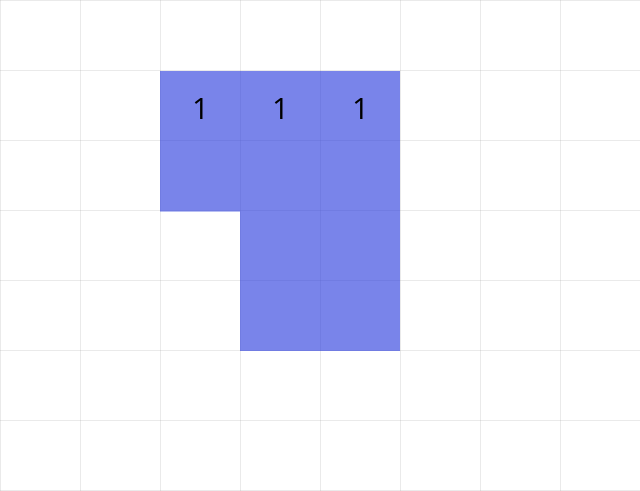
既に安定状態である

Sample3

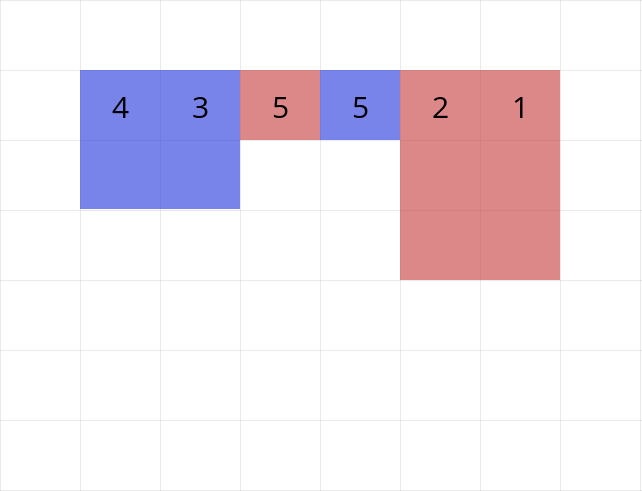
長さ2に揃える．長さ3は全て取り除き，個数が半分より多くなるように長さ1を1つ取り除く．

考察

どの長さで揃えるかを探索する．仮に揃える長さをLと決めた場合，全体のコストの和からLを引き，後は長さLの足の個数-1個分残すようにすればよいとわかる．長さでsortし小さい順から見ていけば，その処理ができる．

揃える長さを緑とした時に，赤の部分は全て取り除くことになる．
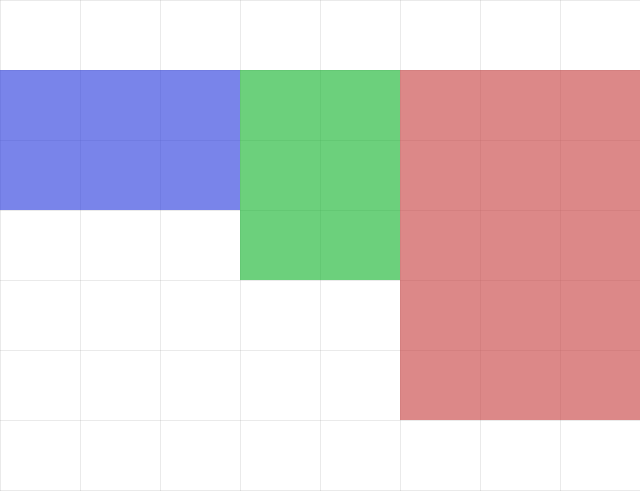
後は緑より小さい足を緑の個数より少なくすればよい．出来るだけコストを抑えたいのでコストが大きい棒を残すようにする．よって全体のコストの和-揃える長さ-(それより長さが短い足をコストの大きい順に個数が少なくなるまで)で求める．

Code

コストが大きい順に見たいためpriority_queueを用いて大きい順に取った．最初は小さい順からとってしまい．WAを生やした．mapを使っているからidなどを作らずにmap巡回をしたほうがより分かりやすい(?)．

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <algorithm>
#include <sstream>
#include <map>
#include <set>
#include <queue>

#define REP(i,k,n) for(int i=k;i<n;i++)
#define rep(i,n) for(int i=0;i<n;i++)
#define INF 1<<30
#define pb push_back
#define mp make_pair

using namespace std;
typedef long long ll;
typedef pair<int,int> P;

int main() {
    int n;
    cin >> n;

    vector<int> L(n),D(n);
    rep(i,n) cin >> L[i];
    rep(i,n) cin >> D[i];

    vector<int> id(L.begin(),L.end());
    sort(id.begin(),id.end());
    id.erase(unique(id.begin(),id.end()),id.end());

    int sum = 0;
    map<int,vector<int> > m;
    rep(i,n) {
        m[L[i]].push_back(D[i]);
        sum += D[i];
    }

    int ans = sum;
    priority_queue<int> que;
    rep(i,id.size()) {
        vector<int> v(m[id[i]].begin(),m[id[i]].end());
        int res = sum;
        int cnt = v.size()-1;

        rep(j,v.size()) res -= v[j];

        vector<int> t;
        while(que.size() && cnt) {
            int q = que.top();
            que.pop();

            res -= q;
            t.push_back(q);
            cnt--;
        }

        ans = min(ans,res);

        rep(j,t.size()) que.push(t[j]);
        rep(j,v.size()) que.push(v[j]);
    }

    cout << ans << endl;

    return 0;
}
Jul 12th, 2015
codeforces